魔の7段階段クイズ答え合わせ

　先日の問題の答え合わせです。未読の方は先にそちらのエントリを読んで考えてから読むことをおすすめします。

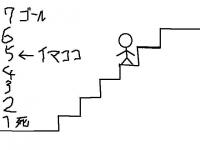
　棒人間君が図のような魔の7段階段の5段目にいます。棒人間君は毎回コインを投げて、表が出れば上に一段登り、裏が出れば下に一段下がります。7段目にたどり着けばクリア、生きて帰れます。逆に1段目まで降りてしまったらゲームオーバー、死にます。

　さて、この棒人間君が生還できる確率は？　もちろんコインの裏表は1/2の確率で等しく出るものとし、階段の途中でやめることはできないものとします。

　さすがネットは広大ですね。3日も経たないうちに解答が出尽くしました。まずもっとも普通に正攻法で解こうとすると、

• 少爺blog’: パズルづいてる2

　となるでしょう。これはもちろん完全に正しくて、正解が出せます。しかしパズルとしてはよりエレガントな解法を見つけたくなると思います。

　問題を読んですぐ一歩引いて「4段目からスタートだったら超簡単なのになあ」と思えた人はセンスがあると思います。

　4段目は階段の中央なので、ルールの対称性より4段目からの生還確率は1/2以外ではありえません。それに気づけば5段目からの生還確率は3段目からの死亡確率に等しいといったことも同時に気がつくでしょう。

　舞台を数直線でなく階段にしたり、棒人間の生死とか大げさな設定をつけたり、一番下を0段目でなく1段目と数えて中央の段を偶数である4にしたりしているのはその対称性から目をそらす策略でもあったわけです。

　時間の対称性にも着目しましょう。時間に応じてルールが変わるわけではないので、コインを振って移動した後も、そこから生還できる確率は最初からそこにいた場合と同じなのです。

　これに気づけば時間tを使った式を立てる必要はなさそうだという予感がしてきます。ここから先の解法はいくつかあるでしょうが、私がもっともエレガントで甲乙つけがたいと思っているのは以下の2通りです。

• Schi Heil と叫ぶために – ビルゲイツの面接試験―株取引編

　この問題の醍醐味をフル活用するとただの連立方程式に。5段目の解を求めるためにあえて一歩引いて他の段からの生存確率を広く考えることでかえって楽に解けてしまうところが素晴らしい。

• 平々毎々

　コイン2回をセットで考えてたまたまそれでうまくいく段数と初期配置だからこその解法というところが、前者に比べて技巧的な印象ではあります。

　しかし、正攻法だとあれほど複雑に見えた問題が、求める確率をそのままxと置いた中学生レベルの方程式1つで解けてしまうというのはある意味感涙モノではないでしょうか。