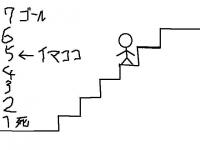
棒人間君が図のような魔の7段階段の5段目にいます。棒人間君は毎回コインを投げて、表が出れば上に一段登り、裏が出れば下に一段下がります。7段目にたどり着けばクリア、生きて帰れます。逆に1段目まで降りてしまったらゲームオーバー、死にます。
さて、この棒人間君が生還できる確率は? もちろんコインの裏表は1/2の確率で等しく出るものとし、階段の途中でやめることはできないものとします。
ボスのビルゲイツの面接試験ネタに便乗してクイズを出してみました。答えはコメントなりトラックバックなりメールなり好きな方法でどうぞ。種明かしと答え合わせは数日後にします。
ちなみに『ビルゲイツの面接試験』の著者ウィリアム・パウンドストーンの本はどれも面白いです。『ライフゲイムの宇宙』『囚人のジレンマ』はおすすめですよ。

コメント
生きるか死ぬかの2択
1/2
期待値を使って
表:裏
生還:死亡
2:4
4/6=2/3
[備忘録]「ビルゲイツの面接試験ネタに便乗」の非数学的?アプローチ
http://tkido.blog43.fc2.com/blog-entry-161.html より via http://sfuhiro.seesaa.net/article/22420470.html 上に行くにも下に行くにも確率は同じなのでこの確率については考えない。 1234567段ある。 4段目から始めれば両者の確率は等しい その着眼点は 123 | 567 で両
あ・・・解りました。
これは、両端への到達の通り数を数える事に意味は無いんですねー。すげー。おもしれー。
Life is..から来ました。
ええと、すいません、まだ良く読んではない無いんですが、単純なイメージとしては、コインの表と裏で進む○段目を樹形図的に追っていくのが正攻法かと思ったら、コインを振る回数の指定が無い為に、スタート→4段目→5段目→4段目→5段目…と永遠に続く事も有り得るわけで、その時点で確率は求められないんじゃないかと思うんですが、この考えは間違ってますか?フェアさんの最初の考えに似てる気がしますが…。
ビルゲイツの面接試験ネタに便乗に便乗の金貨問題
ブログで出題される良問の解答を考えるばかりではと思い、このブログでも問題を出題…
頭の体操:階段死亡遊戯
センスのないタイトルですいません。 http://tkido.blog43.fc…
自己解決しました。
"Life is.."の「亀の子算」の回答編に、自分で考えて解く、ということが書いてありましたね。
はじめまして。Life is beautifulから来ました。
カロンさんの解法と同値ですが、事象を表す二種の記号を定義します。
x->y 状態xの直後が状態yである。
x~>y 状態xの何回か後が状態yである。
求める確率pは、
p = P(5~>7)
= P(5->4~>7) + P(5->6~>7)
= P(5->4~>7) + P(5->6->5~>7)
+ P(5->6->7)
= (1/2)*(1/2) + (1/2)*(1/2)*p
+ (1/2)*(1/2)
これを解いて、p = 2/3となります。
所で、ここでは「マルコフ過程」は禁句なのですか?
ビルゲイツの面接試験―株取引編
とりあえず1問目だけ。 Life is beautiful: ビルゲイツの面接試験―株取引編 パスカルの三角形を書いて考えてたらいい解答を思いついた。 1 1 1 1 2 1 1 3 3 1 n段目にいる時に生還できる確率を と置くと はそれぞれ , と書ける。 を代入して消すと、 で、はど真ん中なので
味もそっけもない解法ですが、
n段目にいる時の生還確率をP(n)とすると
P(1) = 1 (生還!)
P(2) = 1/2×P(1) + 1/2×(P3)
P(3) = 1/2×P(2) + 1/2×(P4)
P(4) = 1/2 (4段目は真ん中だから)
この4つの式を連立させて解くと、
P(3)=2/3
ついでに、
P(2)=5/6
はじめまして、私もLife is beautifulから流れてまいりました。
あちらもそうなんですが、読者へ問題が出されているのを発見した時点で、もうコメントやトラックバックで解答について話がすすんでしまっているのが常ですね。これもほんの足跡がわりということで。
5段から7段へ行くのも3段へ行くのも対称性から五分五分の確率、3段から1段へ行くのも5段へ戻るのも五分五分の確率。
一連の動作で7段へ行くのと1段へ行くのとの確率の比は2:1だった。よって抜け出せる確率は2/3。
私なりにはこんな結論になりました。
しかしUIEJさんは素晴しい人材をそろえていらっしゃるようですね、そっちの方が気になります^^。
ヘンリーの冒険
亀の子算は、難しく考えすぎてしまったので、簡単な解放を探しました。神は細部に宿り給う ビルゲイツの面接試験ネタに便乗棒人間君が図のような魔の7段階段の5段目にいます。棒人間君は毎回コインを投げて、表が出れば上に一段登り、裏が出れば下に一段下がります。7段….
はじめまして、Life is beautiful からきました。
初め、カロンさんとほぼ同じやり方で解いたんですけど、
まだ出てない解法があるってことで、考えてみました。
理論的に怪しげですが、中学生レベルといえばこれでしょう。
【解答】
上に登るのも、下に降りるのも、確率は等しく同じであるのだから、
最上段への到達可能性は純粋にその距離の短さに比例する。
つまり、現在の段から最上段までの距離(段数)と、その到達確率は、
負の比例関係にある。
ここで、
現在の段から最上段までの段数: x
生還できる確率: y
とする。
問題文から、
0 ≦ x ≦ 6
x = 6 のとき y = 0
x = 0 のとき y = 1
であるから、x と y のグラフは
y = -1/6x + 1
となる。
問題では、x = 2 のときの y を求めるのだから、
y = -1/6x + 1 = -1/6 * 2 + 1 = 2/3
よって、棒人間君が生還できる確率は 2/3
魔の7段階段
いい問題だなあ。 以下回答。 この状態から この状態になる確率をxと置く。 「そんな単純なことでいいの?もっと複雑な式を立てるとか……」いいんです。 さて、最初の状態から2回コインを振ったらどうなるか。 「コインは1回ずつじゃないの?」いや、2回のほうが簡単なんh—–
http://tkido.blog43.fc2.com/blog-entry-161.html 棒人間君が図のような魔の7段階段の5段目にいます。 棒人間君は毎回コインを投げて、表が出れば上に一段登り、裏が出れば下に一段下がります。7段目にたどり着けばクリア、生きて帰れます。逆に1段目まで降りてしまったら
今日もまた面白い話題だと思いつつ、私には荷が重いです。
カロンさんの解法を見て思いついた解法はトラックバック先でやられてるし、他の方法は今の所思いつかないですね。
>フェアさん
なぜゆえヘンリー……。
>カロンさん
むう、これは今まで私の頭になかった解法ですなあ。4段目が中心だということを利用したのは素晴らしいです。
ただ前半部は2回セットで考えている最初が表だった場合と、1回振った後の状態で考えている最初に裏が出た場合を一緒に考えていいのか、後半部は最初の状態に戻るものを除いた比率で決めていいかどうか、が必ずしも十分に自明じゃないように思えます。
ちなみに私が最高と考えている2通りの解法のうちのひとつはまだ出てないです。
2回目までのコインの裏表により以下のように算定
a 表表の場合 1/2×1/2=1/4 a
表裏の場合、5段のまま 1/2×1/2=1/4 b
裏の場合、 4段に達し階段の真ん中であるため、生還と死亡の確率は半々。
よって 4段から生還 1/2×1/2=1/4 c
4段から死亡 1/2×1/2=1/4 d
(b)の場合、最初の状態となるため、(b)以外の比率によって生還率が決まる。
よって生還率は、(a+c)/(a+c+d)=2/3 となる。
グハッ・・・
後から間違っていたと思い。修正しようとする前に間違いを指摘されてしまった。まあ私が馬鹿勘違い野郎なのは知ってるさ(ブチブチ
やはりオヤシロさまが書いたのですか。数字がぐにゃぐにゃしてるのがいいのです。
棒人間のことはヘンリーと呼ぶことにしよう
>Satoshiさん
ありがとうございます。対称性とエレガントのキーワードでチョイスしてみました。
>フェアさん
う?ん、それはちょっと問題の意味が理解できていないかも。トラックバック先の少爺blogさんの解答を参考に基本的な考え方を理解してから別解を考えてみてはどうでしょう。
図はペイントで描きました(笑)。
棒人間の生還,別解。
棒人間の生還の中学生でもできそうな(?)別解。 ですが,ちょっと反則であるような気も….
→上に(+1)
コインを投げる →下に(?1)
のように考えると、「生き残る可能性は限りなくある」でしょうか。
たとえ裏を出しても死なない限りは生き残る確立がある上、階段でいつまでも浮き沈みする可能性もあるので可能性が何処までも増えていく……ような気がががが。
いくつも解答方がありそうな雰囲気がムンムン。
ところで棒人間君を書いたのはオヤシロさまでしょうか?数字の部分のイマココとか死のようにシンプルな作りがたまらんのです。
とても良い問題ですね。楽しませてもらいました。寝る前にベッドの中で解こうとしたらムリでした。そこで今日はお昼を食べながら解きました。
パズルづいてる2
棒人間の生還